基于UNet神经网络的城市人流预测
[原创]
1 利用手机信令数据计算人口流动数据
手机信令数据是研究人口的整体流动情况的重要数据来源。移动运营商在为手机用户提供实时通讯服务时,积累了大量的基站与设备的服务配对数据。根据配对和唤醒发生的时间以及基站的地理位置,可以很自然划定一定时间和空间范围,统计每一个时间范围内在特定空间区域内手机设备的停留,进入和离开数据,并据此估算相应的人流数据。
传统的人口网格分析过程一般只关注单个网格内某个时间点人口流动的截面数据以及城市当中不同区域的人口分布统计情况;没有将时间和空间融合考虑,不能对城市整体的人口流动形成一个完整连续的直观描述。但是,作为城市安全运营管理者和规划人员职责是需要把握好城市人口流动规律,建立有效的时空数据分析模型,从而为城市安全运行管理做好相应的人口短时预测与应急管理服务。
2 人口流动数据网格图像流处理
2.1 流处理思路
原始手机信令数据,按照一定的时间间隔(例如15分钟),划分出每个时间段的信令数据情况。主要包括:时间,格网ID,格网中心点经度,格网中心点维度,时间段内格网的停留人数,进入人数,离开人数。
根据原始数据的时空关系,将原始数据转化为4维向量空间矩阵,维度分别为时间维度、空间维度横坐标,空间维度纵坐标以及停留,进入或离开的类别:Matrix[t,i,j,k]=p意味着在t时刻,第i行第j列的空间栅格位置,k=0时则停留人数为p,k=1时则进入人数为p,k=2时则离开人数为p。
在这样的转换关系下,可以将源数据处理为3通道的时空数据。考虑到单个人员流动的时空连续性,可以认为表示人口流通的整体统计量的时空矩阵也具备一定局部关联性,换而言之,一个栅格点的人口流动数据会与该栅格附近的人口流行数据相互关联,也会与前后时间段该栅格的人口流动数据相互关联。而具体的关联形式和影响强度,则需要我们利用卷积神经,对历史数据进行学习来发现和记录相应的关联关系。
更进一步地,通过数据洞察注意到,不同栅格网络间人口流动的时间变化曲线往往倾向于若干种固定模式,直观上,商业区,住宅区,办公区域会呈现出不同的人流曲线变化模式。这种模式与地理位置,用地规划,交通路网信息等属性息息相关。本模型后续将进一步讨论不同用地类型的栅格人口流动模式的比较分析。
| TIME | TAZID | STAY | ENTER | EXIT |
|---|---|---|---|---|
| 2017-04-05 00:00:00 | 1009897 | 460 | 460 | 52 |
2.2 人口栅格数据矢量化
基于一定的空间距离间隔(例如250m),将分析的目标空间划分为若干网格(141*137)。统计T时间内,属于网格M_(p,q)的手机设备停留、进入和离开的数据。按照业务需求,将手机设备数扩样为人口数量,将停留、进入和离开的数据标准化到(0,255)的空间,并将标准化后的数据作为图像的3个颜色通道,据此将T时间的整体网格数据转化为一张三通道格式的图片数据。按照时间维度将经过上述处理的图像作为视频的每一帧图像。
import pandas as pd
import numpy as np
import h5py
# 数据转换成张量类型
data_enter_exit_sz = pd.read_csv('data/sz/data/TBL_ENTER_EXIT_SZ20170401-20170431.csv')
time_list = data_enter_exit_sz['TIME'].unique()
N = len(time_list)
string_to_ix = {string:i for i,string in enumerate(time_list)}
tensor_data = np.zeros([N,141,137,3])
for _,line in data_enter_exit_sz.iterrows():
if int(line['TAZID']) <= 1000000:
continue
x,y = divmod(int(line['TAZID'])-1000000,144)
x = x - 2
y = y - 2
t = string_to_ix[line['TIME']]
tensor_data[t][x][y][0] = line['STAY']
tensor_data[t][x][y][1] = line['ENTER']
tensor_data[t][x][y][2] = line['EXIT']
# 数据保存成h5类型
h5 = h5py.File('model_data/tensor_data_sz.h5','w')
h5.create_dataset('dataset_1', data = tensor_data)
h5.close()
# 数据准备:区分X和Y
h5 = h5py.File('model_data/tensor_data_sz.h5','r')
tensor_data = h5['dataset_1'][:]
h5.close()
M = len(tensor_data)
X = []
Y = []
for i in range(M - 8):
X.append(tensor_data[i:i+8]) # 延迟预测前8个时段预测下1时段
Y.append([tensor_data[i+8][20:120,20:116]]) # 取部分城区
X = np.array(X)
Y = np.array(Y)
# print(X.shape) # (2104, 8, 141, 137, 3)
# print(Y.shape) # (2104, 1, 100, 96, 3)
h5 = h5py.File('./drive/model_data/model_data_sz.h5','w')
h5.create_dataset('date_sz', data=X)
h5.create_dataset('data_sz', data=Y)
h5.close()
将上述处理的网格化人口流动视频流数据作为一个计算机视觉任务,通过计算机视觉算法建立预测模型。在实际运用当中,将会根据一定比例,选定相应的时间点将视频分隔为训练集与测试集。在相应的数据集当中按照一定模式选取相应的帧组合作为模型输入,例如选择T-7到T时刻的数据作为模型输入,来预测T+1时刻的人流网格数据。
3 建立三维U-Net神经网络模型
3.1 人流变化影响因素分析
怎样预测城市中每一个地区的人流量变化是一个困难的问题,本模型在设计方法时,考虑了以下三个方面:
- A.兼顾时间变化的连续性、差异性和周期性。任一地区的人流量变化从时间角度来看一般是连续的,即后一时刻的人流量与前一时刻的人流量关联性最强,而随着时间间隔的增大,两个时刻之间的人流量相关性会逐渐变小。而周期性在不同的时间尺度下还会有所差别:以天为单位观察,我们能看到每天人口从早到晚的涨落;以周为单位观察,我们能看到工作日和周末的明显差异;以年为单位观察,则又能看到四季气候与节假日对人流量的影响。
- B.考虑空间相关性。任何的人流集聚都具有空间相关性:一场社区联欢会能吸引本社区和附近社区的市民参加,一个跨年倒计时可能吸引周边地区乃至全城的人流,一场明星演唱会则会吸引从本市到周边城市乃至全国歌迷的涌入。
- C.考虑各类外部因素影响。如极端天气、节假日、演唱会、球赛、重大活动等,在人流量变化预测的三个关键点中,外部因素的影响需引起重视,这是因为准确把握外部因素对人流的作用是提前化解人口异常集聚问题的前提条件,也是人流量预测的核心价值所在。
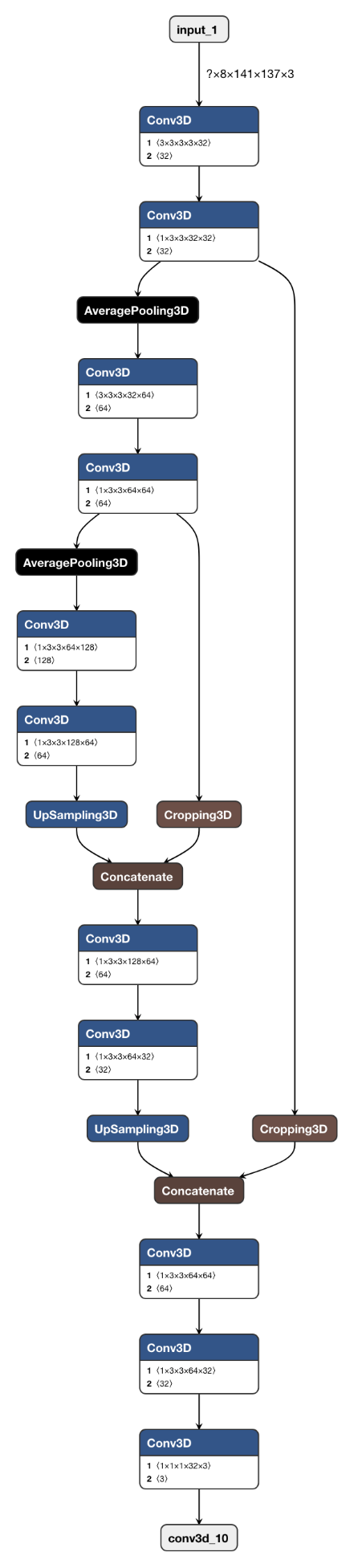
基于上述三个关键点,可以设计了如图所示的U-Net神经网络预测人流量。在这个结构图中:


针对上述A因素,时间依赖性,设计了残差单元,例如,早上8点45分钟发生的交通拥堵会影响上午9点。
针对上述B因素,空间依赖性,设计了U-Net层,例如,地铁系统和高速公路可以带来远距离的依赖性。
针对上述C因素,外部因素影响,设计了全连接层,例如,天气条件和节假日可能会改变人群的流动。
3.2 模型结构框架
U-Net神经网络,结构如图所示,使用卷积层+池化结构提取人流变化的共性模式特征,通过上采样操作将空间维度上被压缩的逐层恢复到原始输入尺寸,并通过相应层级的截取和叠加除了形成同层级的残差结构,保证网络在提取特征的同时充分运用原始图像和空间维度收缩过程中的中间层特征信息。
from tensorflow.keras.layers import Input
from tensorflow.keras.layers import Conv3D
from tensorflow.keras.layers import ConvLSTM2D
from tensorflow.keras.layers import Add
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import AveragePooling3D
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import UpSampling3D
from tensorflow.keras.layers import Cropping3D
from tensorflow.keras.layers import Concatenate
from tensorflow.keras.models import Model
from tensorflow.keras.utils import plot_model
inputs = Input(shape=(8, 141, 137, 3))
conv_1 = Conv3D(filters = 32, kernel_size = (3,3,3),activation = 'relu')(inputs)
conv_2 = Conv3D(filters = 32, kernel_size = (1,3,3),activation = 'relu')(conv_1)
pool_1 = AveragePooling3D(pool_size = (2,2,2))(conv_2)
conv_3 = Conv3D(filters = 64,kernel_size = (3,3,3),activation = 'relu')(pool_1)
conv_4 = Conv3D(filters = 64,kernel_size = (1,3,3),activation = 'relu')(conv_3)
pool_2 = AveragePooling3D(pool_size = (1,2,2))(conv_4)
conv_5 = Conv3D(filters = 128,kernel_size = (1,3,3),activation = 'relu')(pool_2)
conv_6 = Conv3D(filters = 64,kernel_size = (1,3,3),activation = 'relu')(conv_5)
upsample_1 = UpSampling3D(size = (1,2,2))(conv_6)
crop_1 = Cropping3D(cropping = ((0,0),(4,4),(4,4)))(conv_4)
concat_1 = Concatenate()([upsample_1,crop_1])
conv_7 = Conv3D(filters = 64,kernel_size = (1,3,3),activation = 'relu')(concat_1)
conv_8 = Conv3D(filters = 32,kernel_size = (1,3,3),activation = 'relu')(conv_7)
upsample_2 = UpSampling3D(size = (1,2,2))(conv_8)
crop_2 = Cropping3D(cropping = ((5,0),(17,16),(17,16)))(conv_2)
concat_2 = Concatenate()([upsample_2,crop_2])
conv_9 = Conv3D(filters = 64,kernel_size = (1,3,3),activation = 'relu')(concat_2)
conv_10 = Conv3D(filters = 32,kernel_size = (1,3,3),activation = 'relu')(conv_9)
outputs = Conv3D(filters = 3,kernel_size = (1,1,1),activation = 'relu')(conv_10)
3.3 模型评估
将模型输出与实际的T+1数据进行比较,通过Adam,RMSProp等优化器优化迭代神经网络权重,计算误差函数Loss和MAE,如图所示。


3.4 预测结果与实际值比较
| TIME | TAZ_ID | STAY_PRE | ENTER_PRE | EXIT_PRE | STAY_TRUE | ENTER_TRUE | EXIT_TRUE | CENTER_LNG | CENTER_LAT |
|---|---|---|---|---|---|---|---|---|---|
| ####### | 1006550 | 1642 | 53 | 109 | 1661 | 45 | 83 | 120.6351 | 31.15021 |
| ####### | 1010150 | 819 | 40 | 47 | 796 | 16 | 45 | 120.6438 | 31.37676 |
| ####### | 1004550 | 1556 | 79 | 106 | 1559 | 81 | 87 | 120.7985 | 31.01852 |
| ####### | 1010750 | 2225 | 65 | 111 | 2210 | 68 | 107 | 120.8989 | 31.40549 |
| ####### | 1007150 | 1763 | 78 | 116 | 1773 | 101 | 118 | 120.8894 | 31.17894 |
3.5 不同用地性质地块的人口停流量预测结果与实际的比较

3.6 预测后2帧和后4帧
后2帧还行,但是后4帧就会出现不稳定的情况。从现有的数据来看,预测后1帧(15分钟)和后2帧(30分钟)可以达到满意的效果。


4 短期人流预测器产品化解决方案
本模型提出的三维U-Net神经网络可以预知未来一段时间内的城市某些区域人流量变化趋势,这对城市网格化运行管理部门来说无疑增加了一件强大的工具。它可以有效地提高城市的运行效率,更有力地保障城市公共安全。在这一技术的支持下,城市网格化运行管理部门可以提前预知因各类公共事件和突发事件引起的人流快速聚集,从而提前做好相应的疏导、管控和限流等应急预案,最大限度地降低由此带来的负面影响。例如在展会、演唱会和足球赛等场景下,模型的泛化能力能够帮助主办单位对会场周边一定范围内的人流汇聚趋势提前了解,并做好相应安全措施部署,从而保证活动安全有序高效开展。 <
基于Echarts+Mapbox三维GIS可视化展示我们预测的人流24小时实时变化趋势Demo,给前端设计人员提供大屏可视化展示解决方案。
4.1 模型预测结果结构化处理
预测结果数据:

# -*- coding: utf-8 -*-
import pandas as pd
import csv
import json
import h5py
# 矢量化转结构化数据
def make_csv_output(input_matrix,match_csv='.\苏州\data\TBL_ENTER_EXIT_SZ20170405-20170426.csv',start_location=2008,outputs='output_u_net_sz.csv'):
meta_data=pd.read_csv(match_csv,encoding='utf-8',engine='python')
[I,M,N,C]=input_matrix.shape
temp=['TIME','TAZID','STAY','ENTER','EXIT']
for i in range(I):
for m in range(M):
for n in range(N):
if input_matrix[i,m,n,0]!=0 or input_matrix[i,m,n,1]!=0 or input_matrix[i,m,n,2]!=0:
time=meta_data[i+start_location]['TIME']
tzid=(137-m)*117+y+1000000
st=input_matrix[i,m,n,0]
en=input_matrix[i,m,n,1]
ex=input_matrix[i,m,n,2]
temp.append(time,tzid,st,en,ex)
with open(outputs,'w') as f1:
writer=csv.writer(f1)
for line in temp:
writer.writerow(line)
h5f = h5py.File('pre_u_net.h5', 'r')
matrix_data = h5f['dataset_1'][:]
h5f.close()
print(matrix_data.shape)
# make_csv_output(matrix_data)
# 矢量化转成js展示数据格式(下面展示所需要的)
def make_json_output(input_matrix,match_csv='.\苏州\data\TBL_ENTER_EXIT_SZ20170405-20170426.csv',outputs='aaaaaa_output_u_net_sz.json'):
meta_data=pd.read_csv(match_csv,encoding='utf-8',engine='python')
time_list=meta_data['TIME'].unique()
time_ix_to_string={i:string for i,string in enumerate(time_list)}
lat_lon_definition=pd.read_csv('.\苏州\data\苏州TBL_TAZ_DEFINITION.csv',encoding='utf-8',engine='python')
block_id_list=lat_lon_definition[lat_lon_definition['TYPE_ID']==0][['TAZ_ID','CENTER_LAT','CENTER_LON']]
del lat_lon_definition
block_id_list.TAZ_ID = block_id_list.TAZ_ID.astype(int)
block_id_list.set_index('TAZ_ID',inplace=True)
[I,_,M,N,C]=input_matrix.shape
aaa={'type':'FeatureCollection','features':[]}
feature_list=[]
for i in range(24):
bbb={'time':time_ix_to_string[i+8]}
temp=[]
for m in range(M):
for n in range(N):
if input_matrix[i,0,m,n,0]!=0 or input_matrix[i,0,m,n,1]!=0 or input_matrix[i,0,m,n,2]!=0:
ccc={}
tzid=(m+22)*144+(n+22)+1000000
ccc['values']=str([int(input_matrix[i,0,m,n,0]),int(input_matrix[i,0,m,n,1]),int(input_matrix[i,0,m,n,2])])
ccc['lat']=str(block_id_list.at[tzid,'CENTER_LON'])
ccc['lon']=str(block_id_list.at[tzid,'CENTER_LAT'])
temp.append(ccc)
bbb['gridChart_list']=temp
feature_list.append(bbb)
aaa['features']=feature_list
with open(outputs,'w') as f:
json.dump(aaa,f)
h5f = h5py.File('pre_u_net.h5', 'r')
matrix_data = h5f['dataset_1'][:]
h5f.close()
print(matrix_data.shape)
# make_json_output(matrix_data)
4.2 Echarts+Mapbox三维GIS可视化
项目结构:



其中maxbox.html如下所示:
<!DOCTYPE html>
<html style="height: 100%">
<head>
<meta charset="utf-8">
<style>
.echartMap div {
position: absolute;
overflow: auto;
}
</style>
<script src="./lib/echarts.js"></script>
<script src="./lib/mapbox-gl.js"></script>
<script src="./lib/mapboxgl-token.js"></script>
<script src="./lib/echarts-gl.min.js"></script>
<script src="./lib/jquery-2.1.1.js"></script>
<script src="./lib/maptalks.min.js"></script>
<script src="./lib/Tween.js"></script>
<script src="./lib/echarts-gl.1.1.3.js"></script>
</head>
<body style="height: 100%; margin: 0">
<!-- 为ECharts准备一个具备大小(宽高)的Dom -->
<div id="main" style="height: 100%"></div>
<script type="text/javascript">
// 基于准备好的dom,初始化echarts实例
var myChart = echarts.init(document.getElementById('main'))
var uploadedDataURL = "./data/aaaaaa_output_u_net_sz.json";
var MapboxStyleDataURL = "./data/data-1546500855305-wBxWgJRZc.json";
myChart.showLoading();
$.getJSON(MapboxStyleDataURL, function (MapboxStyle) { //读取MapboxStyle数据
var option = {
baseOption: {
timeline: {
axisType: 'category',
orient: 'vertical',
autoPlay: true,
inverse: true,
playInterval: 300,
left: null,
right: 0,
top: null,
bottom: 50,
width: 55,
height: null,
label: {
normal: {
textStyle: {
color: '#fff'
}
},
emphasis: {
textStyle: {
color: '#aaa'
}
}
},
symbol: 'circle',
lineStyle: {
color: '#555'
},
checkpointStyle: {
color: '#bbb',
borderColor: '#777',
borderWidth: 2
},
controlStyle: {
normal: {
color: '#666',
borderColor: '#666'
},
emphasis: {
color: '#aaa',
borderColor: '#aaa'
}
},
data: []
},
title: {
text: "苏州人口分布24小时潮汐",
textStyle: {
color: '#fff',
fontSize: 30
},
right: '5%'
},
visualMap: {
show: false,
calculable: true,
realtime: false,
inRange: {
color: ['#313695', '#4575b4', '#74add1', '#abd9e9', '#e0f3f8', '#ffffbf',
'#fee090', '#fdae61', '#f46d43', '#d73027', '#a50026'
]
},
outOfRange: {
colorAlpha: 0
}
},
maptalks3D: {
center: [120.58319, 31.29834],
zoom: 10,
pitch: 40,
urlTemplate: 'http://{s}.basemaps.cartocdn.com/dark_all/{z}/{x}/{y}.png',
// altitudeScale: 1,
postEffect: {
enable: true,
FXAA: {
enable: true
}
},
light: {
main: {
intensity: 1,
shadow: true,
shadowQuality: 'high'
},
ambient: {
intensity: 0.
},
ambientCubemap: {
texture: './data/data-1491838644249-ry33I7YTe.hdr',
exposure: 1,
diffuseIntensity: 0.5,
specularIntensity: 2
}
}
},
series: [{
type: 'bar3D',
shading: 'realistic',
coordinateSystem: 'maptalks3D',
barSize: 0.5,
silent: true
}]
},
options: [] //timeline所用的多个option存放处,读取数据后添加
}
$.getJSON(uploadedDataURL, function (linedata) { //读取24小时数据
myChart.hideLoading();
var timeline = [];
for (var n = 0; n < linedata.features.length; n++) { //对数据中每天数据整理后添加到options中,以便timeline使用
timedata = linedata.features[n].gridChart_list;
var data = []
var max = linedata.features[n].max;
for (var i = 0; i < timedata.length; i += 1) {
// var _pheight = 1000;
loncol = timedata[i].lon //经度
latcol = timedata[i].lat //纬度
var _v = JSON.parse(timedata[i].values);
var value;
var value = _v[0]; //数组中值相加
count = value;
data.push({
'value': [loncol, latcol, count]
})
}
timeline.push(linedata.features[n].time); //时间(0时到24时)
option.options.push({
visualMap: {
max: 8000
},
series: [{
data: data
}]
});
}
option.baseOption.timeline.data = timeline; //时间轴
if (option && typeof option === "object") {
myChart.setOption(option, true);
}
});
});
// 使用刚指定的配置项和数据显示图表。
// myChart.setOption(option);
</script>
</body>
</html>
